命题逻辑的“原子”:命题
如何表示下述推理?
所有人都是有死的。
苏格拉底是人。
苏格拉底是有死的。
———
p,q├r?
需要深入命题的内部结构——词项逻辑。

词项逻辑就是研究简单命题和简单命题推理的。所谓词项,是指在命题中表示被断定的事物、事物的性质或事物之间的关系的概念。对简单命题和简单命题推理的研究,是建立在对词项的研究基础之上的,因而称为词项逻辑。
简单命题是其本身不再包含其他命题的命题。它不以其他命题为自己的组成部分。简单命题按其断定的是事物的性质还是事物之间的关系,可以分为直言命题(又称性质命题)和关系命题。
词项和概念是逻辑分析的基本单元。在传统逻辑里,词项就是直言命题的主项和谓项;能作为命题的主项和谓项的,都是概念。

命题的基本结构:主谓结构。
词项逻辑关注有如下结构的命题———直言命题:(量项)+主项S+(联项)+谓项P
直言命题断定某种数量的对象具有或不具有某种性质,因此也叫做“性质命题”。
直言命题亦称“定言命题”,即性质命题。由于在性质命题中,对对象具有或不具有某种性质的断定是直接的、无条件的,因而,逻辑史上把这种命题称为直言命题,以别于假言命题(对对象的某种断定是有条件的)和选言命题(对对象的某种断定是有选择的)。把命题分为直言命题、假言命题和选言命题,是从康德开始的。逻辑史上最早详细研究这类命题的是亚里士多德,但他并没有使用“直言命题”这个名称,而称之为简单命题。后来,康德从认识的模态的角度把这类命题叫做实然(原意为断言)命题。传统逻辑学家一般认为,这类命题与选言命题、假言命题不同,它是无条件地、简单地肯定或否定某种事实,因而被汉译为直言命题。
概念:判定(区别、识别)对象。
词项逻辑中,关系、动作都视为一种性质。复合的谓词整体视为一种性质。
联项:肯定的(是)、否定的(不是)
量项:由量词充当。根据是否断定主项外延的全体,分为全称的与特称的。
全称量词:所有、全部、每个……
特称量词:有的、有些、某些……
不区分单数与复数,不排斥全称量词(从弱原则),不处理广义量词:大多数、近半数、少数、极个别。
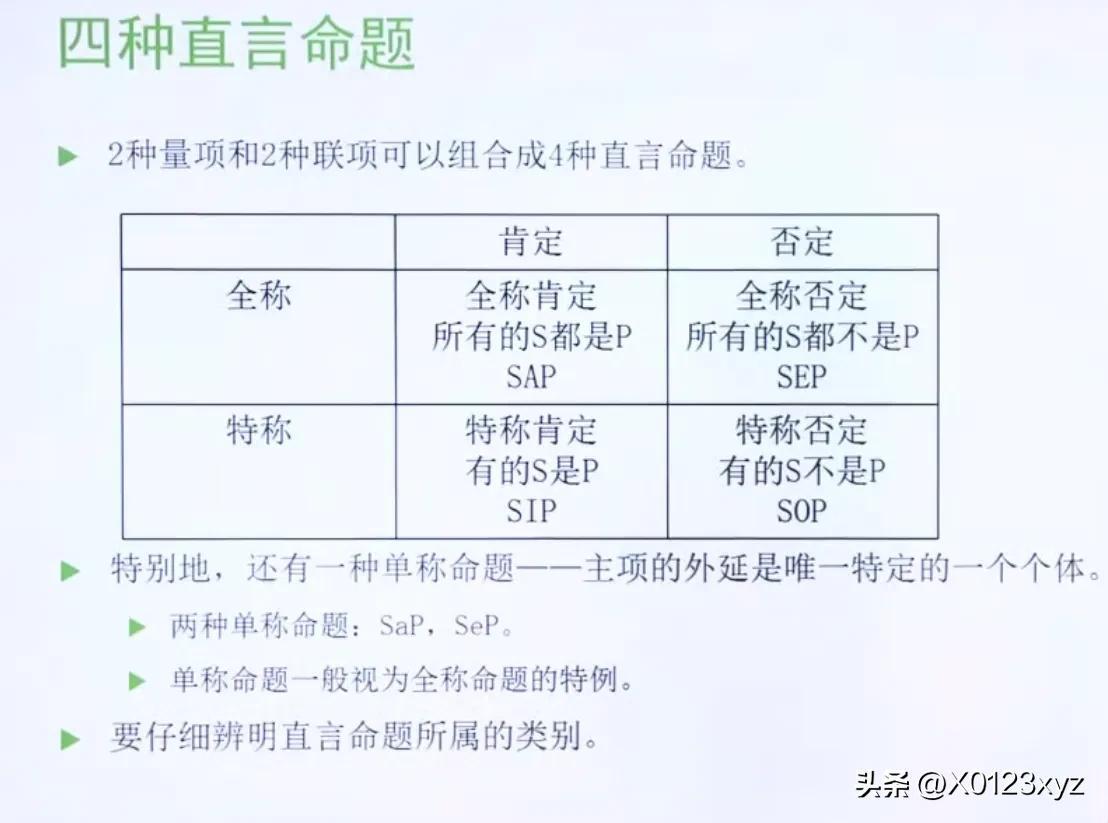
直言命题中主谓项的关系
一个词项既有内涵,也有外延,内涵是词所表达的意义,外延是词所指示的对象。现在经典逻辑(或说通用逻辑)里的主项与谓项都只考虑其外延意义。
主项与谓项的外延:集合(类)。
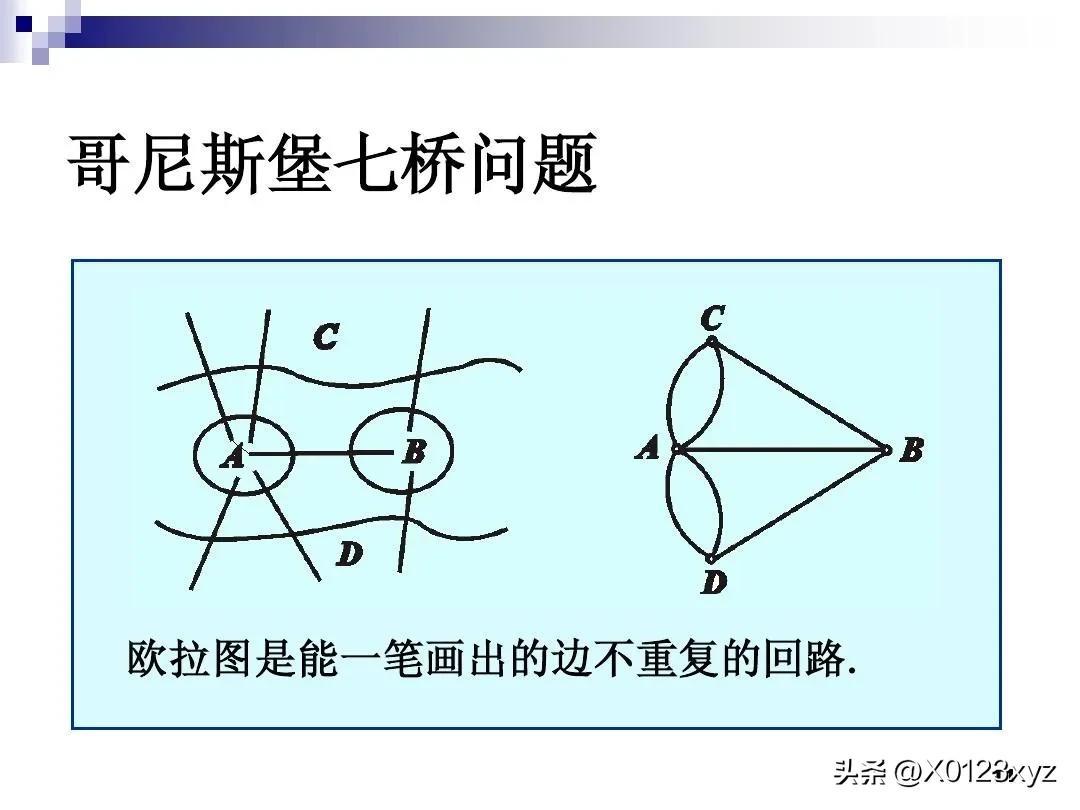
欧拉图是由瑞士数学家欧拉(Leonhard Euler,1707~1783)发明的,后人曾加以改进,它用圆圈表示非空非全的类或集合之间的关系。
主项与谓项的关系,实质上是两个非空集合间的关系。两个概念之间有如下五种关系:同一关系、包含关系、包含于关系、交叉关系、全异关系。

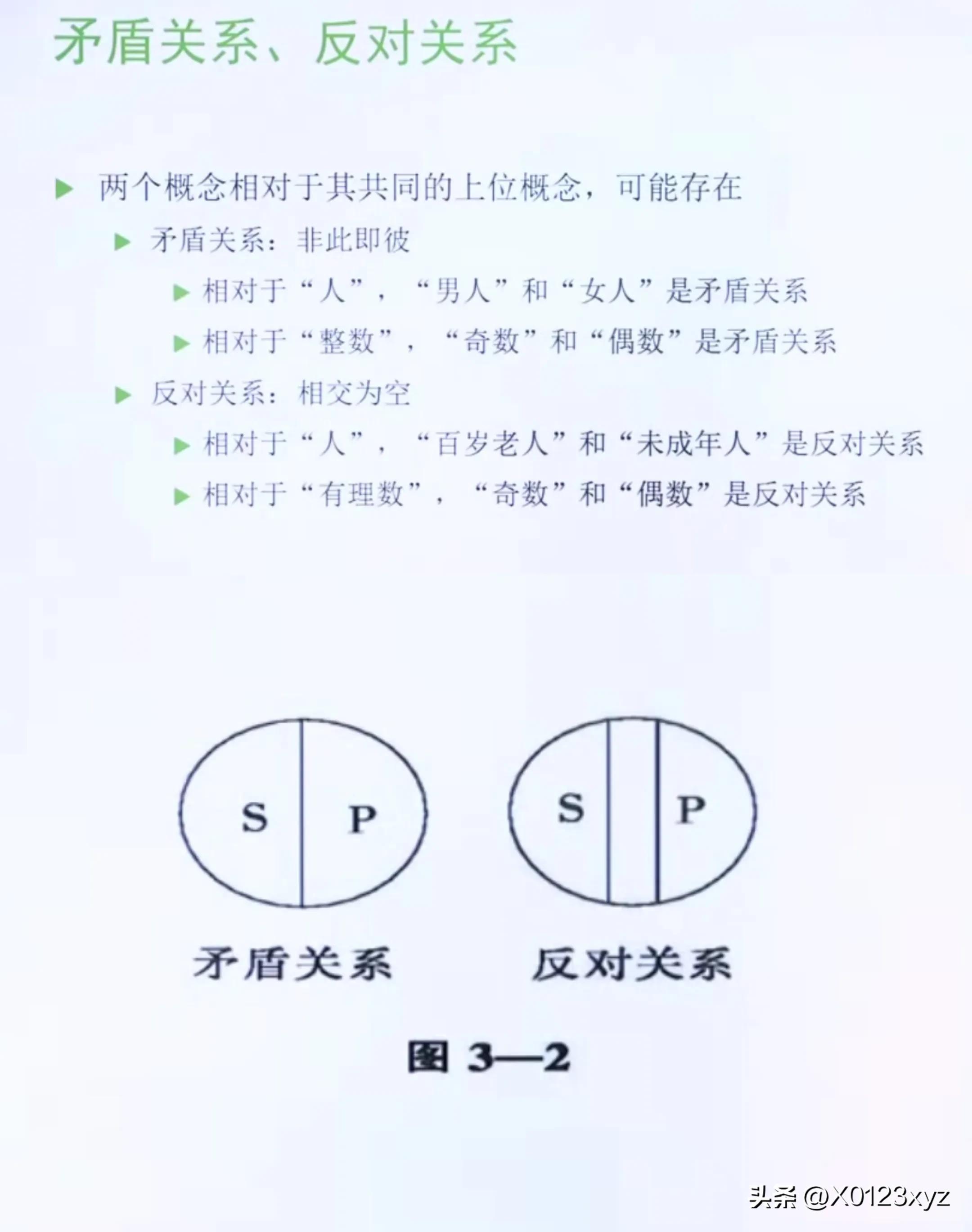
根据直言命题的主谓项相对于第三个概念(上位概念)的关系,全异关系可以再区分为矛盾关系(例如相对于人类,男人和女人的关系)和反对关系。
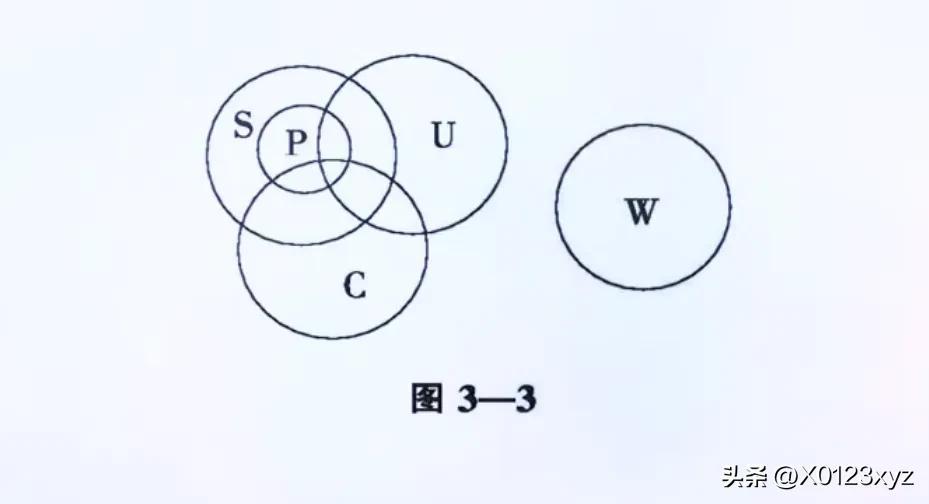
多个概念之间的外延关系,实际上只不过是两个概念之间外延关系的复杂化,即逐一考察其中每两个概念之间的关系,然后把考察的结果组合起来。例如,“大学生”(S)、“北大学生”(P)、“中国人”(C)、“共产党员”(U)、“北京大学”(W)这一组概念之间的关系可以图示如下:
一个直言命题,无非是对主项和谓项外延关系的一种断定或者取舍,它有真假。在主谓项五种可能的关系中,直言命题的真值状况如下:
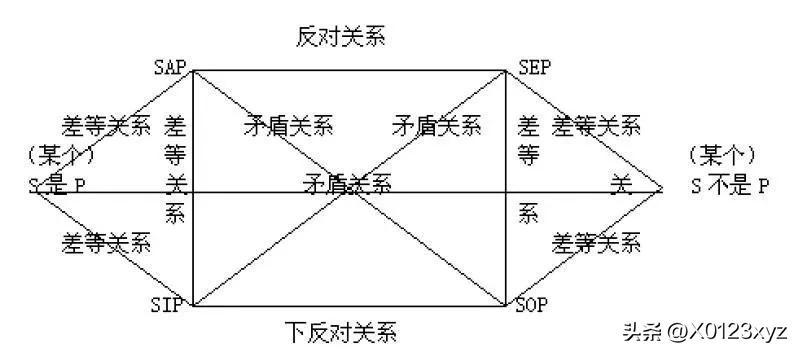
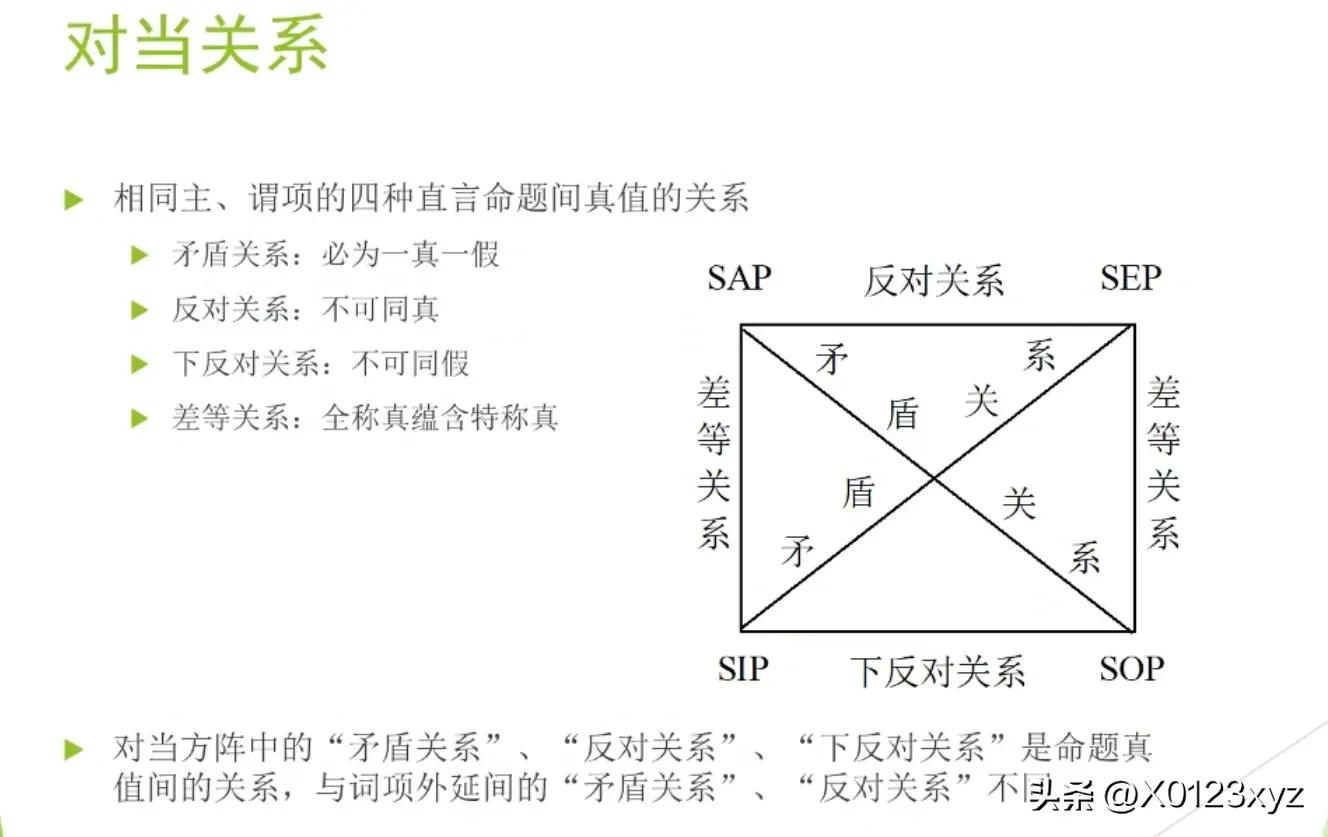
对当关系(opposition)简称“对当”,是具有相同主谓项的A、E、I、O判断之间的真假关系。包括;1.矛盾关系:不能同真,不能同假。存在于A和O及E和I之间;2.从属关系,亦称差等关系,即蕴涵关系,存在于A和I及E和O之间;3.反对关系:不能同真,可以同假。存在于A和E之间;4.下反对关系:可以同真,不能同假。存在于I和O之间。
周延性
周延性:在给定的直言命题中,词项是否断定全体外延的性质。(“周遍外延”)
全称命题的主项周延,特称命题的主项不周延。
肯定命题的谓项不周延,否定命题的谓项周延。
SAP———S周延,P不周延
SEP———S周延,P周延
SIP ———S不周延,P不周延
SOP———S不周延,P周延
